Step by step guide

In this step by step problem solving guide for the Imat exam , we will explore various types of questions found in the problem solving subsection and the skills they aim to assess. Each explanation will be accompanied by an example and a breakdown of the solution, with an emphasis on the solving techniques employed.

Additionally, we will provide a general approach to addressing these questions, focusing on how to recognize the consistent framework or “skeleton” behind them and how to adapt to the variables, or additional information, that is introduced within the framework.

Identifying Patterns and approach to Problem Solving Questions

Mastering the art of identifying patterns in problem-solving questions is a crucial skill that can greatly improve your ability to solve problems efficiently and accurately. This comprehensive guide will walk you through a systematic approach to identifying patterns in various types of questions, providing examples to help you internalize the information effectively and apply it to your problem-solving endeavors.

Step 1: Understand the Problem

The first step in identifying patterns is to gain a thorough understanding of the problem at hand. Read the question carefully and pinpoint the key information provided. Determine the category of the question you are dealing with (e.g., ratio, minimum and maximum, decryption, etc.) so you can employ suitable strategies and techniques.

Step 2: Break Down the Problem

To make the problem more manageable, break it down into smaller, more digestible components. This process will allow you to identify patterns and relationships within the problem more easily. Pay attention to similarities or recurring elements in the structure of the problem, as they may indicate the presence of a pattern.

Step 3: Analyze Relationships

Investigate the relationships between the various elements in the problem. For instance, if you’re working on a ratio question, concentrate on how the values are related proportionally. Gaining a solid understanding of these relationships will enable you to discern patterns that can aid you in solving the problem effectively.

Step 4: Test Cases and Simplify

Utilize test cases, if applicable, to uncover patterns in the problem. Begin with basic examples to develop your understanding of the underlying patterns. Once you’ve detected a pattern, you can extend its application to more intricate situations.

Step 5: Generalize and Apply

After you’ve identified a pattern, formulate a generalized version that can be applied to a broader array of scenarios. This generalization will not only help you solve the current problem but also equip you with the tools to tackle similar problems in the future with increased efficiency.

In conclusion, becoming proficient in pattern recognition for problem-solving questions involves a methodical approach that entails understanding the problem, breaking it down, analyzing relationships, testing cases, and generalizing the pattern for application in various contexts. By following these steps and practicing regularly, you’ll develop the skills necessary to solve problems effectively and efficiently, ultimately enhancing your problem-solving abilities.

Types of problem solving questions on the IMAT 

Interpreting Graphs

Interpreting graphs aims to assess your ability to read and analyze visual data representations. This type of question might require you to identify trends, make predictions, or compare different data sets.

Common traps and strategy for resolution: A common trap in interpreting graphs is misinterpreting units of measurement or scale on axes, which can lead to inaccurate conclusions. Ignoring important information provided in the legend or labels can also be problematic.

To avoid these traps, it’s essential to focus on understanding various types of graphs and their components, such as axes, legends, and units of measurement. Practice reading and interpreting data to enhance your visualization skills and be mindful of the larger context.

Example :

The bar chart below shows the number of endangered species between 2000 and 2002 per animal class.

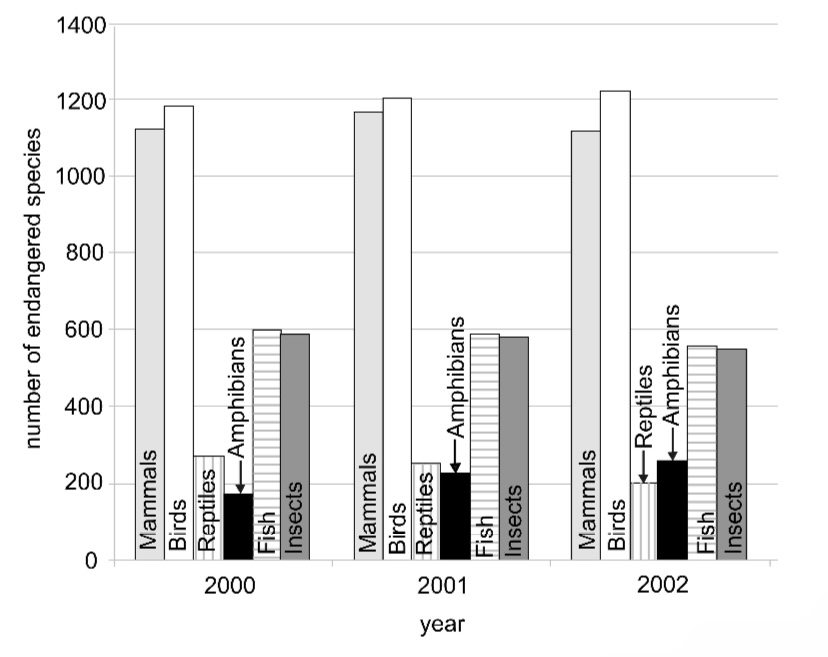
Which one of the following pieces of information can be inferred from the bar chart above?

A. The number of species of insects that were endangered was almost equal to the number of species of fish that were endangered over the three-year period.

B. The number of endangered species of mammals remained constant over the three-year period.

C. The number of endangered species of reptiles increased over the three-year period while that of amphibians decreased.

D. In 2001, there were exactly four times as many endangered species of birds as there were endangered species of reptiles.

E. More species of bird became endangered over the three-year period than any other animal class.

Solution : 

1.understand the problem at hand ; read the question part first and then the presentation of the given information (in this case it’s in a graph) . underline key information

2.Breakdown the answers. Simplify, put in simple words on emphasis of the relationship between the pieces of information.

3. Look for the answer that corresponds with the relationship established.

4.  Make sure to use the chosen answer to describe the info given in the graph as a double check. In this case the correct answer will be A.

Processes questions

Ratio problem solving

Ratio questions evaluate your understanding of relationships between quantities, proportions, and rates. You might be asked to simplify ratios or solve problems involving proportionality.

Visualize ratios as two objects of different sizes, with the size difference representing the relationship between the quantities.

Common traps and strategy for resolution: Test creators may lay traps in ratio questions by including irrelevant or misleading information, providing complex ratios or decimals to distract the test-taker, or creating ambiguous comparisons that can lead to incorrect conclusions.

To avoid these traps, test-takers should practice manipulating and comparing ratios, identify the relevant information, and understand the rules and properties of ratios. They should be mindful of any conflicting or ambiguous information and try to simplify the problem to its core elements.

Example : 

Tom shared out some money between his three children in the ratio 5:3:2. He later had an extra €6 which he gave to the child who received the least originally. This meant that the money had been shared into one large and two equal smaller shares.

How much money in total did Tom give to the three children?

A. €36
B. €26
C. €60
D. €20
E. €66

Solution : 

To solve this problem, follow these steps:

1. Identify key information:
   • Original ratio: 5:3:2
   • Extra €6 given to the child with the least amount
   • Resulting in one large and two equal smaller shares
2. Determine the objective: Find the total amount Tom gave to the three children.
3. Set up an equation using the information:
   • Let 5x, 3x, and 2x represent the original amounts given to the children.
   • After giving an extra €6 to the child with the least amount, the two smallest shares become equal. So, 3x = 2x + €6.
4. Solve the equation:
   • Subtract 2x from both sides: x = €6
5. Find the original amounts given to the children:
   • 5x = 5(€6) = €30
   • 3x = 3(€6) = €18
   • 2x = 2(€6) = €12
6. Calculate the total amount : what was given to the three children, including the extra €6:
   • Total amount = €30 + €18 + €12 + €6 = €66

The answer is E, €66. Tom gave a total of €66 to the three children.

Elimination with Constraints

Eliminations and constrains questions assess your logical reasoning and ability to deduce solutions by narrowing down possibilities based on given conditions.

Imagine this skill as a detective carefully eliminating suspects based on clues, leading to the correct solution.

Common traps and strategy for resolution: A common trap in elimination with constraints questions is ignoring or overlooking some of the constraints or conditions provided in the problem, which can lead to incorrect solutions. Jumping to conclusions too quickly or failing to use logical reasoning to eliminate possibilities can also be problematic.

To avoid these traps, it’s essential to practice using logical reasoning to eliminate options based on constraints and make inferences. Break the problem down into smaller parts and consider each constraint separately before making decisions.

Example : 

When riding my bike in the dark, I use two rear bike lamps. Both of the lamps are in ‘flashing mode’, which means that they repeatedly emit light for a set period of time at set intervals. The reasons for using two lights are that it reduces the amount of time when neither of the lamps emit light, and that if one of the lamps stops working, other road users can still see me on the road. One of the lamps shines for one second and goes dark for one second repeatedly; the other lamp shines for two seconds and goes dark for two seconds repeatedly.

I always turn both lamps on simultaneously at the start of my ride.
For how many seconds in each minute do neither of the lamps shine when they are in use?

A 10

B 12

C 15 

D 20 

E 30

Solution : 

1. Identify key information:
   • First lamp: shines for 1 second, goes dark for 1 second
   • Second lamp: shines for 2 seconds, goes dark for 2 seconds
   • Both lamps are turned on simultaneously
   • Objective: Find the number of seconds in each minute when neither lamp shines
2. Determine the pattern of both lamps:
   • First lamp (1 second on, 1 second off): On-Off-On-Off…
   • Second lamp (2 seconds on, 2 seconds off): On-On-Off-Off…
3. Identify when both lamps are off at the same time:
   • We will consider the least common multiple (LCM) of the two cycles, which is 4 seconds (1-second cycle for the first lamp and 2-second cycle for the second lamp).
   • In every 4-second interval:
     • First lamp: On-Off-On-Off
     • Second lamp: On-On-Off-Off
   • Both lamps are off simultaneously in the third second of every 4-second interval.
4. Calculate the number of seconds when neither lamp shines within a minute:
   • There are 60 seconds in a minute, and each 4-second interval contains one second when both lamps are off.
   • 60 seconds ÷ 4-second intervals = 15 intervals
   • Both lamps are off simultaneously for 1 second in each interval: 15 intervals × 1 second = 15 seconds

The answer is C, 15 seconds. In each minute, neither of the lamps shines for 15 second

Minimum and Maximum:

Minimum and maximum questions measure your optimization skills by asking you to identify the lowest and highest values under specific constraints.

Visualize this skill as a mountain range with valleys (minimums) and peaks (maximums) to be discovered within given conditions.

Common trap and strategy for resolution:A common trap in minimum and maximum questions is overlooking constraints or conditions that affect minimum or maximum values, which can lead to incorrect solutions. Failing to consider all possible values or solutions or misinterpreting the problem and solving for the wrong values can also be problematic.

To avoid these traps, always read the actual question that’s being asked first and underline key information. It’s essential to practice solving optimization problems and finding the minimum and maximum values within given conditions. Consider all possible solutions and double-check your calculations to avoid errors.

Example :

A factory has received an order for a product. It takes 9 operations to manufacture it. These may take place in any order and at any time in the manufacturing process but an individual worker stays with one operation from its beginning to its end. The number of hours for one worker to complete each operation is as follows:

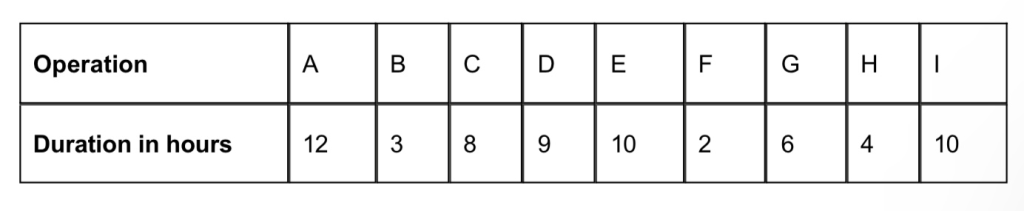
All workers are able to complete all operations, but can only do one at a time. The product has to be ready in 16 hours.

What is the minimum number of workers required to manufacture the product in the given time?

A. 6
B. 4
C. 9
D. 1
E. 5

Solution : 

To solve this problem, follow these steps:

1. Identify key information:
   • Different tasks with varying hours
   • Objective: Find the minimum number of workers needed to complete all tasks in a 16-hour workday
2. Determine the approach:
   • Examine the given hours for each task
   • Add as many hours as it takes to reach 16 or as close to 16 as possible, aiming to find which workers can do more than one job in the allotted time
   • By doing this, we find the minimum number of workers by wasting the least amount of hours possible
3. Combine tasks based on their hours:
   • Tasks A (12 hours) and H (4 hours): 12 + 4 = 16 hours
   • Tasks E (10 hours) and G (6 hours): 10 + 6 = 16 hours
   • Tasks B (3 hours), F (2 hours), and I (10 hours): 3 + 2 + 10 = 15 hours
4. Keep track of the completed steps and mark them off on the exam paper.
5. Tasks C (8 hours) and D (9 hours) are left, but they cannot be completed together:
   • Task C: 8 hours
   • Task D: 9 hours
6. There is no other rearrangement that could give us any fewer workers.

Therefore, the answer is 5, as the minimum number of workers needed to complete all tasks in a 16-hour workday is 5.

Spatial Reasoning:

Spatial reasoning questions test your ability to visualize and manipulate spatial relationships between objects in 2D and 3D contexts.

Imagine this skill as a Rubik’s cube, requiring mental manipulation of shapes and patterns to solve problems.

Common traps and strategy for resolution: A common trap in spatial reasoning questions is mislabeling or misidentifying shapes, which can lead to incorrect solutions. Additionally, failing to visualize shapes or transformations accurately or misapplying formulas or rules for 2D or 3D shapes can also cause issues.

To avoid these traps, it’s important to hone your spatial reasoning skills by working with various shapes and visualizing relationships between objects. Practice mentally manipulating 2D and 3D shapes and identifying common geometric properties. Additionally, it can be helpful to draw diagrams or sketches to help visualize and solve problems more effectively.

Example :

The following pattern is made from six square tiles:

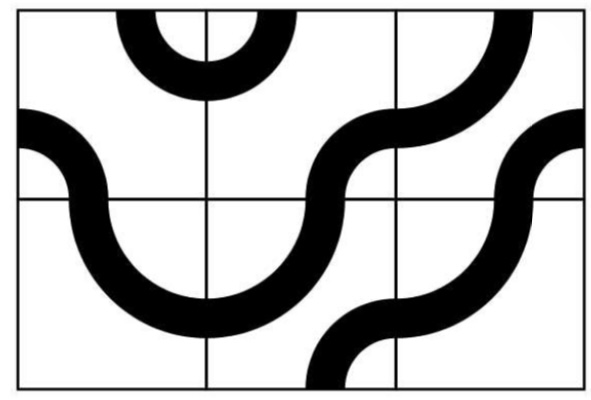
Which one of the following patterns can also be made from the same six tiles?

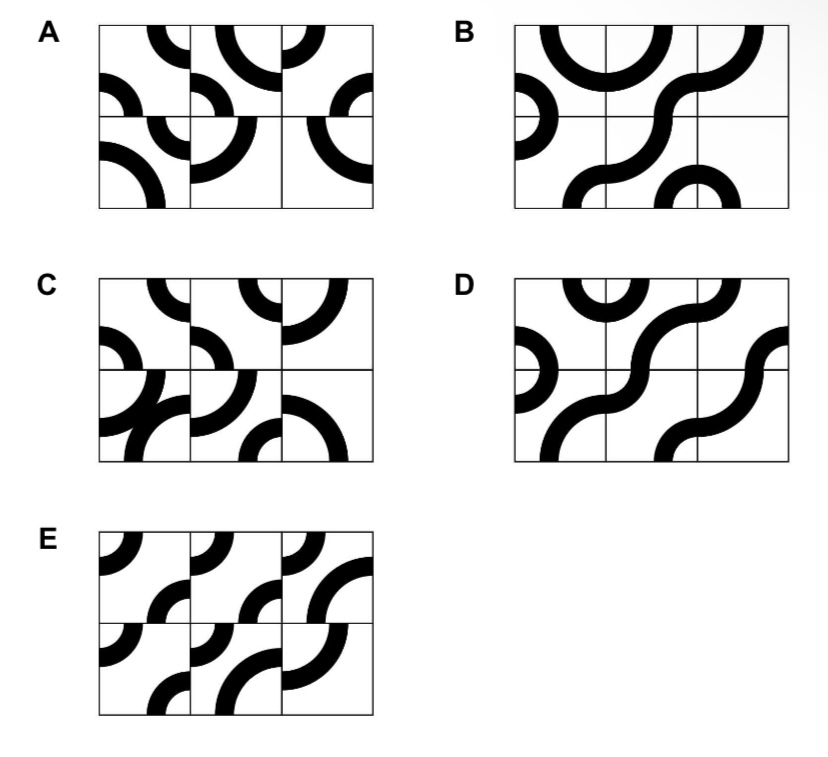
Solution : (general for tile 2D)

For 2D tile problems, the general approach can be adjusted as follows:

1. Identify key information:
   • Read the problem carefully and note any important information about the tiles, such as their shapes, sizes, or colors
   • Pay attention to any specific rules or constraints related to arranging or fitting the tiles
2. Visualize the problem:
   • Sketch a simple diagram or grid to represent the space or pattern in which the tiles need to be arranged
   • This will help you understand the spatial relationships between the tiles and any constraints on their placement
3. Determine the approach:
   • Understand what the question is asking and identify the strategy or strategies that might be helpful in solving the problem
   • This might include using geometric principles, analyzing patterns, or employing a trial-and-error method
4. Break down the problem:
   • Divide the problem into smaller, more manageable parts if possible, such as focusing on one section of the space or one type of tile at a time
   • Work systematically and logically to explore different arrangements or combinations of tiles
5. Test possible solutions:
   • Place the tiles in various configurations, using logical reasoning and deduction to determine which arrangements satisfy the given constraints or rules
   • Eliminate options that do not fit the given constraints or rules, and continue testing until a valid solution is found
6. Review and confirm the solution:
   • Once you have arrived at a solution, double-check your work and ensure that it satisfies all given constraints and rules
   • If the solution doesn’t seem to fit, revisit your approach and try another strategy if necessary . 

In this case the answer is A.

Comparing Savings :

Comparing savings questions evaluate your financial analysis skills by requiring you to analyze different financial scenarios and determine the most beneficial option.

Visualize this skill as a scale, weighing the pros and cons of different financial options to find the best choice.

Common traps and strategy for resolution: To lay traps in comparing savings questions, test creators may include misleading or irrelevant information to distract the test-taker from the critical details. They may also provide unclear information or add unnecessary steps to the problem-solving process.

To avoid these traps, test-takers should practice comparing interest rates, investment options, and discount offers, identify the relevant information and terms, and understand the rules and properties of financial scenarios. You should be mindful of any conflicting or ambiguous information and try to simplify the problem to its core elements. Finally, double-checking all calculations and assumptions can ensure that the solution aligns with the given constraints and conditions.

Example :

In a family, each of the six children has one packet of crisps on each weekday (Monday to Friday) for their packed lunch. The triplets have Cheese flavored crisps, the twins have Paprika flavored crisps, and the oldest child always has Chilli flavored crisps. The exact number of packets of crisps needed are purchased at the same time for the four-week period.

The table below shows the price of single packets of crisps and multipacks of crisps of the same flavor. A multipack is a discounted collection of a number of single packets of one flavor.

Packet Type	Price
Single Packet	£0.50
Multipack of 6	£2.50
Multipack of 12	£4.50
Multipack of 24	£8.50
Multipack of 36	£12.50

What is the most money that can be saved for the four weeks by purchasing the appropriate combination of multipacks and single packs of the different flavors rather than all single packs?

A. £43.50
B. £23.50
C. £8.00
D. £18.00
E. £16.50

Solution :

1. Identify key information and underline.
2. Determine the question’s objective.
3. Eliminate non-essential information.
4. Use a visual aid such as a picture, graph, or equation (simplify the data).
5. Work on paper writing the steps to avoid mistakes, especially during exams.
6. Solve the problem.

For this problem, we need to find the difference in cost between buying discounted packs and non-discounted packs. To do this, we’ll first calculate the cost of buying only single packs, and then find the cheapest combination of packs.

Organize the information:

• Triplets (3 children): need 60 bags (3 x 20 days)
• Twins (2 children): need 40 bags (2 x 20 days)
• Single child: needs 20 bags (1 x 20 days)

Calculate the cost for each combination:

• Triplets: 1 multipack of 36 (£12.50) + 1 multipack of 24 (£8.50) = £21.00
• Twins: 1 multipack of 36 (£12.50) + 4 single packets (£0.50 each) = £14.50
• Single child: 1 multipack of 12 (£4.50) + 1 multipack of 6 (£2.50) + 2 single packets (£0.50 each) = £8.00

Total cost of the cheapest combination: £21.00 + £14.50 + £8.00 = £43.50

Calculate the cost of buying only single packs: £0.50 x 120 packs = £60.00

Price difference: £60.00 – £43.50 = £16.50

Therefore, the answer is E, £16.50

Scoring:

Scoring questions test your ability to calculate and compare scores in different contexts, such as weighted averages or rankings.

Visualize this skill as a leaderboard where scores need to be calculated, compared, and ranked to solve problems.

Common traps and strategy for resolution: Test creators may lay traps in scoring questions by including complex ranking or scoring systems that require logical reasoning to understand. They may also provide misleading or irrelevant information, such as adding unnecessary or irrelevant criteria, to confuse the test-taker.

To avoid these traps, test-takers should practice solving problems related to scoring systems, understand the rules and properties of rankings and tiebreakers, and identify the relevant information. They should be mindful of any conflicting or ambiguous information and try to simplify the problem to its core elements.

Example :

A golf tournament is played over 10 rounds, on successive Saturdays. The winner of each round scores 3 points and the player finishing second scores 1 point. The tournament is won by the competitor with the most points over the 10 rounds.
Alan Vinci, Barry Durand, Carl Johansson and Daniel and Eric Lim were the participants in this year’s tournament. All five won at least one round, but either Barry, Daniel or Eric finished second on each occasion. The 1­-2 finishing order was different every round, and the Lim brothers didn’t both score points in the same round at any time.

Who won this year’s tournament?

A. Eric Lim
B. Daniel Lim
C. Barry Durand
D. Carl Johansson
E. Alan Vinci

Solution:

1.Identify key information:

• 10 rounds, winner gets 3 points, second place gets 1 point
• Participants: Alan Vinci, Barry Durand, Carl Johansson, Daniel Lim, Eric Lim
• All five won at least one round
• Second place: Barry, Daniel, or Eric
• 1-2 finishing order different every round
• Lim brothers didn’t both score points in the same round

2.Determine the approach:

• We need to find the winner of the tournament by considering the given information and constraints.
• Analyze possible point distributions based on the given conditions.

3.Break down the problem:

• All five participants won at least one round, so they all have at least 3 points.
• There are 10 rounds, so there are 10 winners and 10 second-place finishers.
• Since the Lim brothers never both scored points in the same round, they each won and came second in different rounds.
• Let’s consider the point distribution for each participant.

4.Test possible solutions:

• Let’s try to allocate the wins and second places for each player, taking into account the given constraints.

Alan Vinci: Won at least 1 round = 3 points
Barry Durand: Won at least 1 round and finished second in some rounds = 3 points + (1 point * number of second places)
Carl Johansson: Won at least 1 round = 3 points
Daniel Lim: Won at least 1 round and finished second in some rounds = 3 points + (1 point * number of second places)
Eric Lim: Won at least 1 round and finished second in some rounds = 3 points + (1 point * number of second places)
Since there are 10 rounds, and we know that all players won at least 1 round, we have 5 wins already allocated. That leaves 5 more wins to be distributed among the players.

Logical reasoning:

• Since Alan and Carl only won 1 round each, they cannot win the tournament as they have only 3 points each.
• Now, we are left with 5 wins to distribute between Barry, Daniel, and Eric.
• The maximum points any of them can score is if one of them wins all the remaining 5 rounds (3 points each) and finishes second in all the other rounds (1 point each), totaling 18 points.
• Thus, the maximum points for any of Barry, Daniel, and Eric are 18 points.
• However, the Lim brothers never scored points in the same round, so the maximum points for either of them would be when one of them wins 5 rounds and the other wins none of the remaining rounds, giving them 15 points.

Review and confirm the solution:

• Alan Vinci and Carl Johansson both scored only 3 points, so they cannot win the tournament.
• The Lim brothers can score a maximum of 15 points each.
• Barry Durand can score a maximum of 18 points.

Thus, the winner of the tournament is Barry Durand (C).

In conclusion, becoming proficient in pattern recognition for problem-solving questions involves a methodical approach that entails understanding the problem, breaking it down, analyzing relationships, testing cases, and generalizing the pattern for application in various contexts. By following these steps and practicing regularly, you’ll develop the skills necessary to solve problems effectively and efficiently, ultimately enhancing your problem-solving abilities.

Efficiently identifying patterns in problem-solving questions is not only about mastering the techniques but also about managing time and stress effectively. In addition to the systematic approach outlined earlier, this guide will provide tips for time management, optimization of efficiency, and stress management in the context of pattern recognition and problem-solving.

Time and stress Management, Optimizing Efficiency 

1. Prioritize tasks: Begin by solving questions that appear less time-consuming or those you feel more confident about. This strategy helps build momentum and ensures you secure some points early on.
2. Set time limits: Allocate a specific amount of time for each question and track your progress. This approach will prevent you from spending excessive time on a single problem, allowing you to address all questions within the given timeframe.
3. Practice regularly: Regular practice enhances your pattern recognition skills and enables you to solve problems more efficiently. Time yourself during practice sessions to develop a better sense of timing and pacing.
4. Keep it organized: Maintain an organized workspace and have all necessary resources readily available. This practice minimizes distractions and ensures a smoother problem-solving process.

Stress Management:

1. Stay calm and focused: Take deep breaths and remind yourself of your preparation and abilities. Keeping a clear head will enable you to approach problems more effectively.
2. Breaks and self-care: Don’t forget to take short breaks during extended problem-solving sessions. Use this time to relax, stretch, or have a snack. Ensuring you are physically and mentally refreshed will contribute to better focus and performance.
3. Positive mindset: Maintain a positive attitude and avoid negative self-talk. Embrace challenges as opportunities to learn and grow. Believe in your ability to solve problems, and remember that practice will lead to improvement.
4. Visualize success: Take a moment to visualize yourself successfully solving problems and identifying patterns. This mental exercise can boost your confidence and help reduce anxiety.

In summary, developing expertise in pattern recognition for problem-solving questions involves not only mastering the techniques but also managing your time and stress effectively. By prioritizing tasks, setting time limits, practicing regularly, staying organized, maintaining a positive mindset, and taking care of yourself, you can optimize your efficiency and overall problem-solving experience. Combining these tips with the previously outlined systematic approach will lead to improved performance and success in solving problems.

Helpful videos and links

You can practice from Oxford TSA past papers, so the past Imat papers can be used as simulations

https://www.admissionstesting.org/for-test-takers/thinking-skills-assessment/tsa-oxford/preparing-for-tsa-oxford/